KDTree

Posted on 2024-06-27 Edited on 2024-07-08 In 数据结构与算法 Views:

2k 词 9 分钟

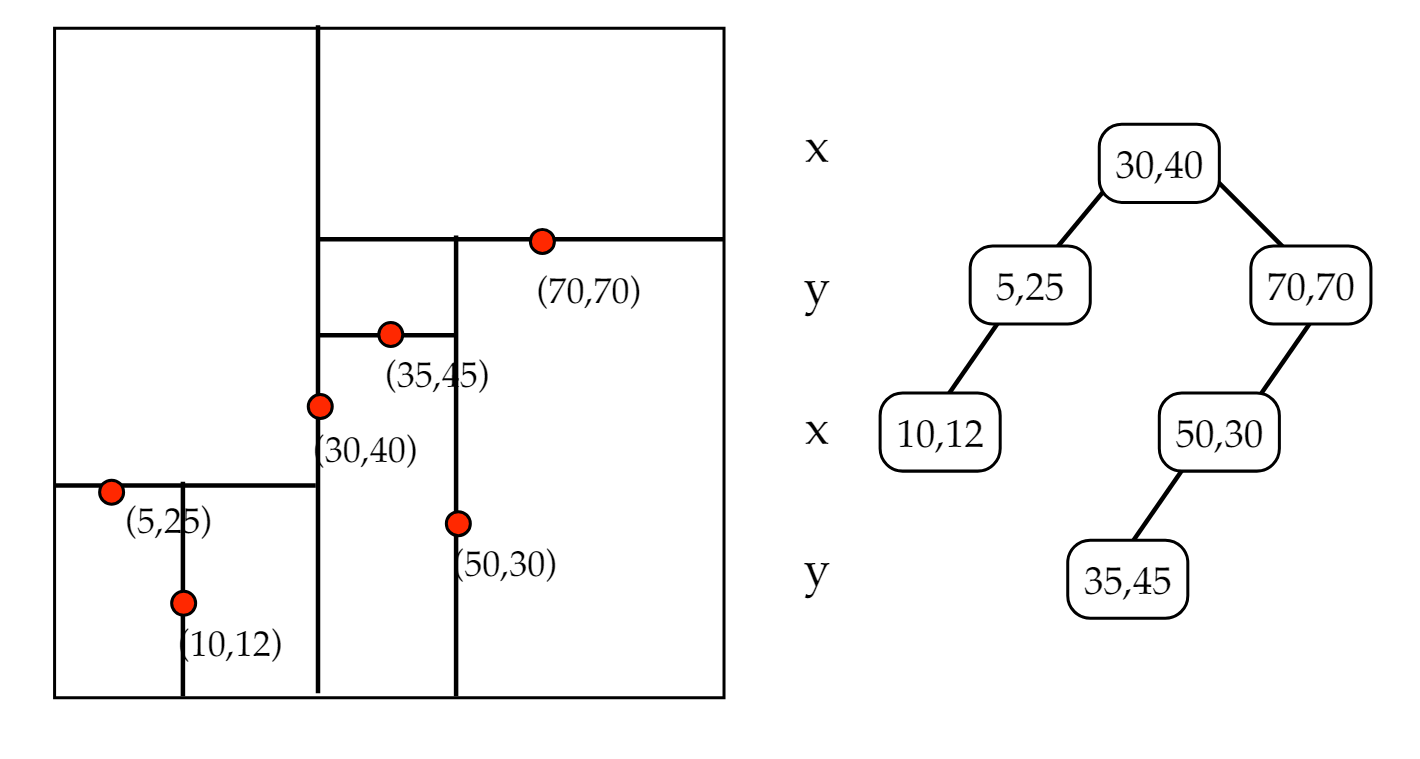
什么是KDTree

KDTree 是一种树数据结构，用于存储多维数据，是二叉搜索树(BST)的推广，广泛应用于查询操作。KDTree表示数据的维数必须全部相同，KDTree是每个节点都为k维点的二叉树。所有非叶子节点可以视作用一个超平面把空间分割成两个半空间。节点左边的子树代表在超平面左边的点，节点右边的子树代表在超平面右边的点。选择超平面的方法如下：每个节点都与k维中垂直于超平面的那一维有关。因此，如果选择按照x轴划分(如图1 (30,40节点)，所有x值小于30的节点都会出现在左子树，所有x值大于等于30的节点都会出现在右子树。这样，超平面可以用该x值来确定，其法线为x轴的单位向量。下一层，按照y轴划分(如图1 (5, 25节点)，所有y值小于25的节点放在左子树，大于25的放在右子树。以此类推，KDTree根据深度选择分割超平面，设深度为level，数据维数为dim。则分割超平面用第level % dim维的值来确定。图2是三维KDTree。

图1 二维KDTree

图2 三维KDTree

KDTree的运算

建树

struct Node {
	double coordinate[DIM];

	Node(double coordinate[]) {
		for (int i = 0; i < DIM; i++){
			this->coordinate[i] = coordinate[i];
		}
	}

	Node() {
        for (int i = 0; i < DIM; i++) {
            this->coordinate[i] = 0;
        }
    }

	bool operator == (const Node & node) {
		for (int i = 0; i < DIM; i++) {
			if (this->coordinate[i] != node.coordinate[i]) {
				return false;
			}
		}
		return true;
	}

	friend std::ostream& operator << (std::ostream& os, Node node) {
		os << "(";
		for (int i = 0; i < DIM; i++) {
			os << node.coordinate[i] << " ";
		}
		os << ")";
		return os;
	}

};

struct kdNode {
	Node data;
	kdNode* left, *right;

	kdNode() : left(nullptr), right(nullptr) {};
	kdNode(const Node node, kdNode* L = nullptr, kdNode* R = nullptr) {
		data = node;
		left = L;
		right = R;
	}
};

插入

插入操作和BST类似，只不过比较的是第level % dim维的值。

kdNode* insert(Node x, kdNode* t, int cd) {
	if (t == nullptr){
		t = new kdNode(x);
	}
	else if (x == t->data) {
		return nullptr;
	}
	else if (x.coordinate[cd] < t->data.coordinate[cd]) {
		t->left = insert(x, t->left, (cd + 1) % DIM);
	}
	else {
		t->right = insert(x, t->right, (cd + 1) % DIM);
	}
	return t;
}

寻找最小值

寻找最小值定义为：寻找在第d维值最小的点。
步骤：

如果当前搜索维数 == d，则根据KDTree性质，最小值不可能在右子树。判断左子树是否存在，若存在，递归搜索左子树；若不存在，返回根节点。

如果当前搜索维数 != d，则最小值可能在左子树，根节点或右子树，递归搜索，最后从三个结果中选取最小值。

Node* findmin(kdNode *T, int dim, int cd) {
	if (T == nullptr) {
		return nullptr;
	}
	if (cd == dim) { // 搜索维数 == d
		if (T->left == nullptr) { // 左子树不存在
			return &T->data;
		}
		else { // 递归搜索左子树
			return findmin(T->left, dim, (cd + 1) % DIM);
		}
	}
	else { // 递归搜索左右子树
		Node* a= findmin(T->left, dim, (cd + 1) % DIM);
		Node* b = findmin(T->right, dim, (cd + 1) % DIM);
		Node* c = &T->data;
    
    // 选取最小值
		return minnum(a, b, c, cd); 
	}
}

Node* minnum(Node* node1, Node* node2, Node* node3, int cd) {
    Node* minNode = nullptr;
    int minCoordinate = std::numeric_limits<int>::max(); // 初始化为最大整数值

    if (node1 != nullptr && node1->coordinate[cd] < minCoordinate) {
        minNode = node1;
        minCoordinate = node1->coordinate[cd];
    }
    if (node2 != nullptr && node2->coordinate[cd] < minCoordinate) {
        minNode = node2;
        minCoordinate = node2->coordinate[cd];
    }
    if (node3 != nullptr && node3->coordinate[cd] < minCoordinate) {
        minNode = node3;
        minCoordinate = node3->coordinate[cd];
    }

    return minNode;
}

删除

步骤：

设待删节点为A, 当前所处于第d维。
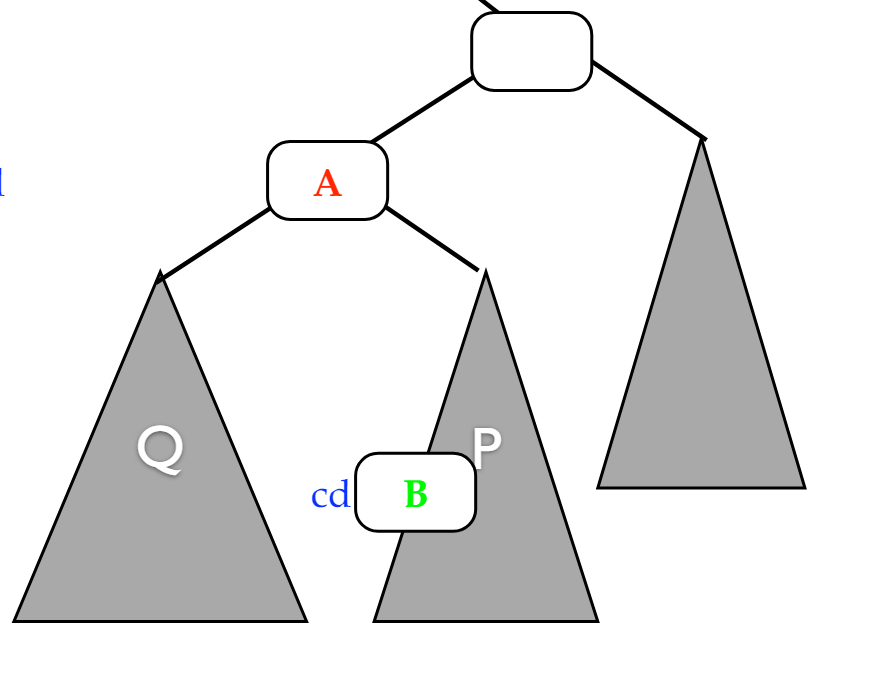
如果待删节点右子树存在，搜索右子树d维最小值节点B，替换节点A，如此左子树所有节点第d维数据均小于节点B，右子树所有节点第d维数据均大于等于节点B(如图3)。
如果待删节点左子树存在，右子树不存在，交换左右子树，同上。
如果子树为空，则为叶子节点，直接删除

图3

kdNode* delete_node(Node x, kdNode* t, int cd) {
	int next_cd = (cd + 1) % DIM;
	if (t == nullptr){
		cout << "error";
		return t;
	}

	if (x == t->data) {
		// 如果右子树不为空，findmin(t.right, cd), 找到右子树当前维度最小值，与待节点交换, 删掉待节点。 
		if (t->right != nullptr) {
			t->data = *findmin(t->right, cd, next_cd);
			t->right = delete_node(t->data, t->right, next_cd);
		}
		// 如果右子树为空，find(t.left, cd), 找到左子树当前维度最小值，与待节点交换, 删掉待节点，将将左右子树交换。
		else if (t->left != nullptr) {
			t->data = *findmin(t->left, cd, next_cd);
			t->right = delete_node(t->data, t->left, next_cd);
			t->left = nullptr;
		}
		// 叶节点
		else {
			t = nullptr;
		}
	}
	else {
		if (x.coordinate[cd] < t->data.coordinate[cd]) {
			t->left = delete_node(x, t->left, next_cd);
		}else {
			t->right = delete_node(x, t->right, next_cd);
		}
	}
	return t;
}

最近邻搜索

定义：最邻近搜索用来找出在树中与输入点(Qurey)最接近的点。注意：空间中的最近点，可能在树中距离远。

方法：
遍历所有节点，使用两个方法进行剪枝

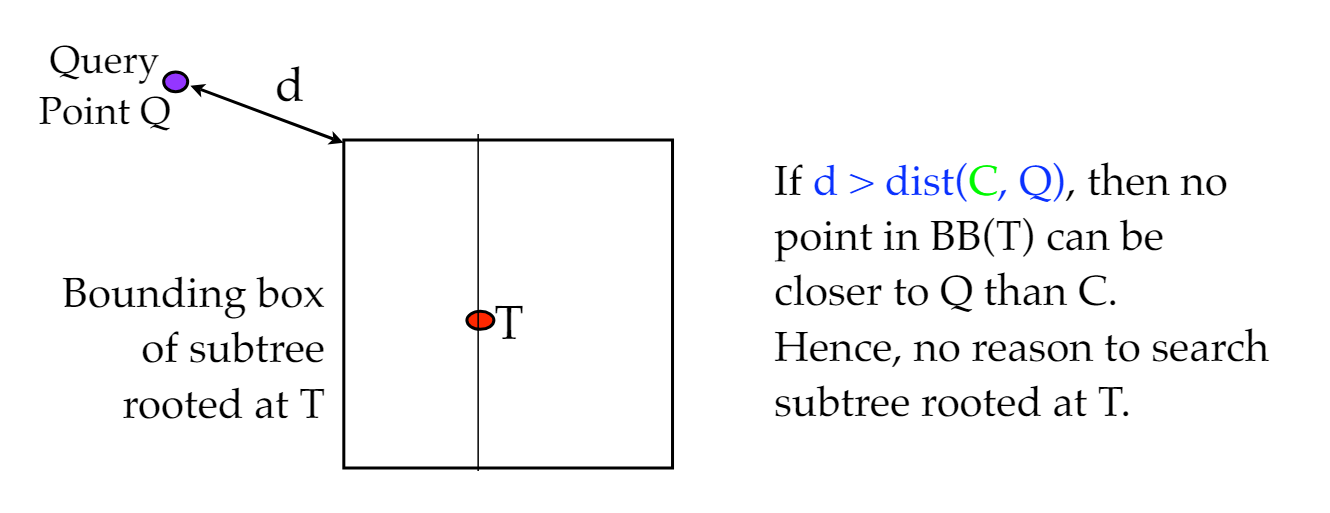
维持一个最近节点C，最近距离d，搜索节点时定义边界框，当边界框中所有节点最近距离不可能小于d时，剪枝(如图4)。
以最大化剪枝机会的顺序搜索。

图4

首先定义边界框Rect类

struct Rect {

	double mincoords[DIM]; // 最小边界
	double maxcoords[DIM]; // 最大边界

	Rect(double mincoords[], double maxcoords[]){
		for (int i = 0; i < DIM; i++){
			this->mincoords[i] = mincoords[i];
			this->maxcoords[i] = maxcoords[i];
		}
	}
	// 在左子树中搜索，则将最大边界更新为根节点相应维度的值
	Rect trimleft(int cd, double value) {
		double new_coords[DIM];
		for (int i = 0; i < DIM; i++){
			new_coords[i] = maxcoords[i];
		}
		new_coords[cd] = value;
		return Rect(mincoords, new_coords);
	}
  // 在右子树中搜索，则将最小边界更新为根节点相应维度的值
	Rect trimright(int cd, double value){
		double new_coords[DIM];
		for (int i = 0; i < DIM; i++){
			new_coords[i] = mincoords[i];
		}
		new_coords[cd] = value;
		return Rect(new_coords, maxcoords);
	}
};

搜索函数

Node* best_node = nullptr; // 最近点
double best_distance = DBL_MAX;  // 最近距离

void search_neighbor(Node* query, kdNode* T, int cd, Rect BB){
  // 如果T为空，或者query与边框距离大于best_distance返回
	if (T == nullptr || ((distance(query, new Node(BB.mincoords)) > best_distance) && (distance(query, new Node(BB.maxcoords)) > best_distance))){
		return;
	}
  // 更新
	double dist = distance(query, &T->data);
	if (dist < best_distance) {
		best_distance = dist;
		best_node = &T->data;
	}

  // 如果当前维度query值 < 根节点值.根据KDTree特征，先搜索左子树，后搜索右子树
	if (query->coordinate[cd] < T->data.coordinate[cd]) {
		search_neighbor(query, T->left, (cd + 1) % DIM, BB.trimleft(cd, T->data.coordinate[cd]));
		search_neighbor(query, T->right, (cd + 1) % DIM, BB.trimright(cd, T->data.coordinate[cd]));
	}
   // 如果当前维度query值 < 根节点值.根据KDTree特征，先搜索右子树，后搜索左子树
	else {
		search_neighbor(query, T->right, (cd + 1) % DIM, BB.trimright(cd, T->data.coordinate[cd]));
		search_neighbor(query, T->left, (cd + 1) % DIM, BB.trimleft(cd, T->data.coordinate[cd]));
	}
}

sklearn实现

import numpy as np
from sklearn.neighbors import KDTree
rng = np.random.RandomState(0)
X = rng.random_sample((10, 3))  # 10 points in 3 dimensions
tree = KDTree(X, leaf_size=2)              
dist, ind = tree.query(X[:1], k=3)                
print(ind)  # indices of 3 closest neighbors
print(dist)  # distances to 3 closest neighbors

处理高维数据

维数灾难让大部分的搜索算法在高维情况下都显得花俏且不实用。同样的，在高维空间中，k-d树也不能做很高效的最邻近搜索。一般的准则是：在k维情况下，数据点数目N应当远远大于${\displaystyle 2^{k}}$时，k-d树的最邻近搜索才可以很好的发挥其作用。不然的话，大部分的点都会被查询，最终算法效率也不会比全体查询一遍要好到哪里去。另外，如果只是需要一个足够快，且不必最优的结果，那么可以考虑使用近似邻近查询的方法。